So I decided to solder my circuit onto a new board so that I don't need to worry about bad connections. Guess what? The new board couldn't work, not even the first stage of the circuit, the DIY instrumentation amplifier. When I set both input voltages at 0, it outputs a 5V high-frequency oscillation, which I couldn't explain. I need to a fine-tuned instrumentation amplifier!
So I waited for my AD620 to come for about a week. I followed some advice online and changed my circuit:
Coming out of the in-amp, the signal will go through a high-pass filter, a buffer, a second-order low-pass filter and a 60Hz "Twin-T" notch filter.
Interesting thing about this circuit is that the drifting of the voltage level, which was a major problem for my previous circuit, is now gone. The voltage level will always stay around 0V (or any voltage I want), which is great for microcontroller sampling because it never goes out of the range of 0-5V. The downside of the circuit is that when the signal stays at some voltage level (e.g. when the user is staring at some angle), the output voltage decays to zero within maybe 100ms (half period depends on circuit design). So I would need to use some algorithm to recover the signal.
The up-left graph is the Vout of the circuit. When I roll my eyes to the right, Vout goes up. If we zoom in, we will see that the signal decays exponentially to the reference point after each peak, which means that at "free fall" (when Vin doesn't change), dVout/dt = C0 * (Vout - C1), where C0 is a constant that can be measured, and C1 is equal to the bias voltage I set. So in order to recover the signal, I can calculate dVout/dt, add back the "free-fall decay speed" of C0 * (Vout-C1) to get dVin/dt, and then do integral of dVin/dt to get the orientation of the eye. The up-right graph is the Vin recovered by algorithm above.
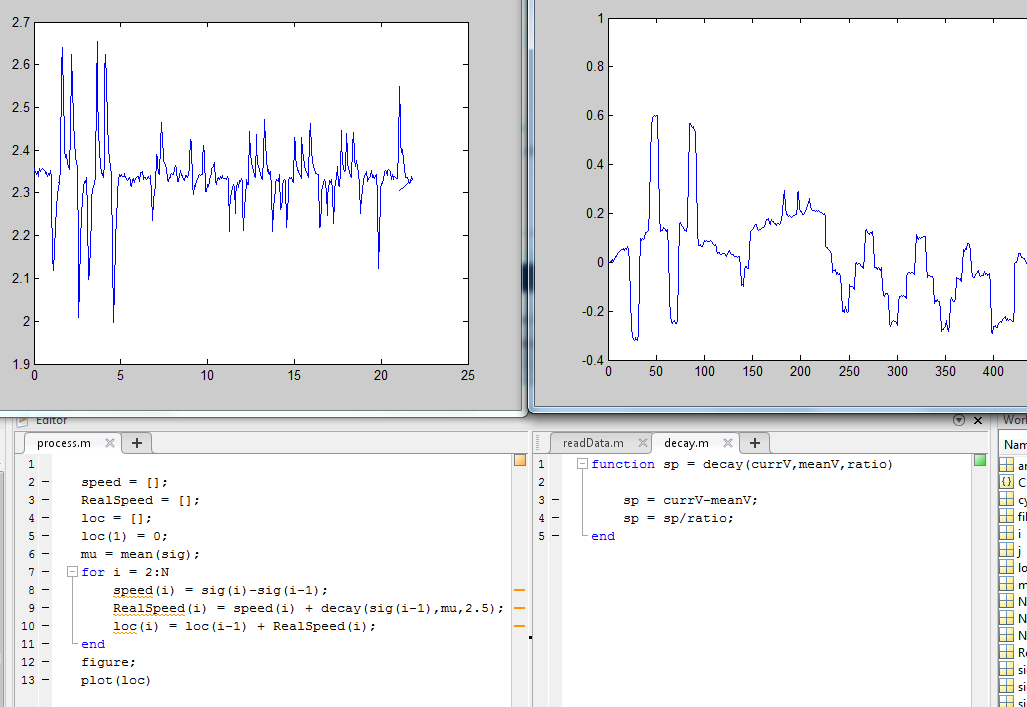
However, the algorithm doesn't work as nicely as above every time. See the following as an example:
The problem is that there's still the annoying drifting. Over about 10 seconds the random drift could account for as much as 50% of the output, which means that if the output changes by 100, the actual signal could have changed by any number between 50 to 100. This accuracy is unacceptable!
Also, there's the problem of choosing C1 (the reference voltage). Since there's the integral step in my algorithm, changing C1 by 0.01V would cause a massive drift of the output. It becomes really hard to let the micro-controller set the reference voltage correctly in the algorithm when it's real-time. How do i get that reference voltage, which is supposed to be constant but is actually different across different tests for unknown reasons? Average algorithm would be problematic when the signal is not symmetric.
So I decided to give up this circuit! This theory is beautiful, but there's always the distance between theory and reality.
New circuit:
Not so different. Just that the high-pass filter and the buffer are gone. I tried this circuit and found that the drifting became really small in short period of time. Why much smaller than the circuit I used two weeks ago? I guess on that circuit I had too many cascaded RC low-pass filters, and they were cascaded without any buffer in between, so the cut-off frequency was actually much lower than what I calculated.(lowered to around 4Hz instead of the 16Hz that I intended) This would cause the drift to be relatively bigger than the EOG signal since drifting usually has a much lower frequency. And when I had 10 RC LPF cascaded like that, it's no surprise that I got a crazy 5V drift when the EOG signal is just about 200mV. With the new circuit, the cut-off freq stays at 16Hz. As a result, the drift and the EOG signal are "treated" quite equally. Over about a minute the drift could be around 0.1V - 0.2V when the signal is at 0.5V.
Although this is much better than before, I still need to work on this for the next week. So far I have tried some algorithms to eliminate noise and drifting of the HPF. For example I took the speed at each point and filter out all the low-speed points. This would filter out most of the noise and drifting, but due to the exponential decay property of that HPF circuit, some of the low-speed points play an important part in the recovery algorithm. Without them I will always under-compensate for the decay and thus the drift of reference. I guess it won't be such a big problem for the new circuit since it doesn't have that exponential decay property. I will put this part in the final post after I finish more testing on noise elimination, smoothing, and the final wrap-up. Check out Yifan's post for our milestone demo! It's really cool to see the robot's eyes move in the same way my eyes do!
Although this is much better than before, I still need to work on this for the next week. So far I have tried some algorithms to eliminate noise and drifting of the HPF. For example I took the speed at each point and filter out all the low-speed points. This would filter out most of the noise and drifting, but due to the exponential decay property of that HPF circuit, some of the low-speed points play an important part in the recovery algorithm. Without them I will always under-compensate for the decay and thus the drift of reference. I guess it won't be such a big problem for the new circuit since it doesn't have that exponential decay property. I will put this part in the final post after I finish more testing on noise elimination, smoothing, and the final wrap-up. Check out Yifan's post for our milestone demo! It's really cool to see the robot's eyes move in the same way my eyes do!



No comments:
Post a Comment